T3C02 - Énergie mécanique
Travail d'une force
Définition
Soit un système modélisé par un point M dans un référentiel galiléen soumis à une force \(\vec{F}\).
Le travail d'une force correspond à l'énergie fournie par une force pour effectuer un déplacement entre deux points A et B \[W_{A \to B} (\vec{F}) = \vec{F} \cdot \vec{AB} = F \times AB \times \cos \alpha\] où α est l'angle entre \(\vec{F}\) et \(\vec{AB}\), F est la force en newton (N) et AB est la distance en mètre (m).
Le travail est homogène à une énergie, il s'exprime donc en joules (J).
- Si α ∈ [0; 90[ : W > 0, le travail est moteur
- Si α = 90 : W = 0, le travail est nul
- Si α ∈ ]90; 180] : W < 0, le travail est résistant
6, 7 p 268
Énergie cinétique
Définition
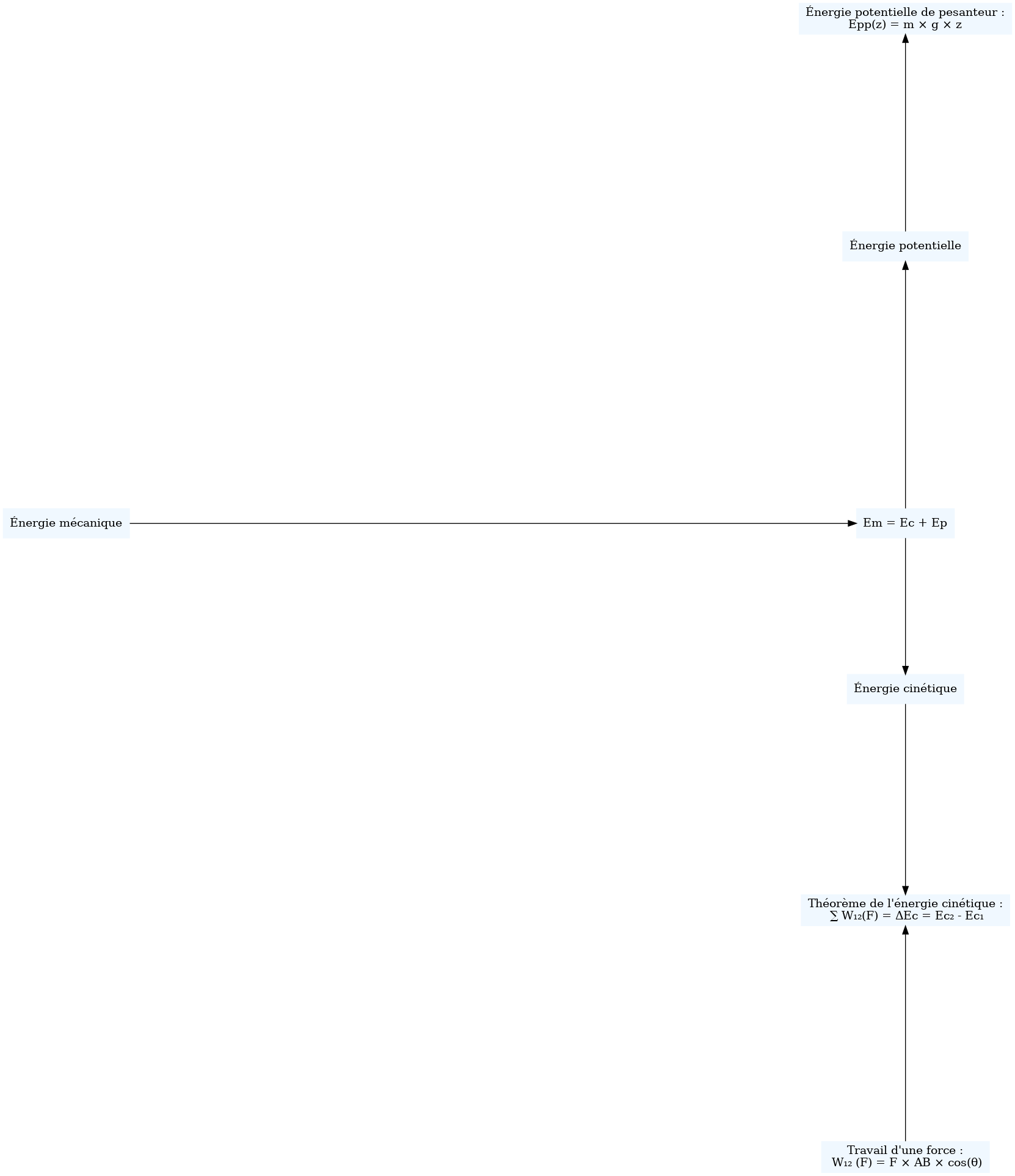
Soit un système de masse m se déplaçant à la vitesse v dans le référentiel R, son énergie cinétique est \[E_c = \dfrac{1}{2} \times m \times v^2\] où Ec est l'énergie cinétique en joules (J), m en kg, v en m ⋅ s-1.
3, 5 p 268
Théorème de l'énergie cinétique
Dans un référentiel galiléen, la variation d'énergie cinétique entre deux points A et B est égale au travail de la force résultante : \[W_{A \to B} (\vec{F}) = E_C(B) - E_c(A)\]
8 et 9 p 268
Énergie potentielle
Force conservative
Si le travail d'une force ne dépend que de sa position de départ et de sa position d'arrivée, alors la force est conservative.
- Le poids est une force conservative, son travail ne dépend que des altitudes de départ et d'arrivée
- La force électrostatique est une force conservative
- La force de frottement n'est pas conservative, elle dépend de la longueur du trajet
Énergie potentielle
Si une force est conservative, alors elle dérive d'une énergie potentielle Ep1.
L'énergie potentielle indique la quantité d'énergie qu'un système peut potentiellement utiliser pour se mettre en mouvement ou pour subir une transformation.
La seule énergie potentielle à connaître en première est l'énergie potentielle de pesanteur : \[E_{pp} = m \times g \times z\] où g est l'intensité de la pesanteur terrestre (en m/s2), m la masse du système (en kg) et z son altitude (en m)
Le poids dérive de l'énergie potentielle de pesanteur Epp = m × g × z, preuve \[-\dfrac{\partial E_p}{\partial z} = -m \times g\] soit \(\vec{P} = -m \times g \times \vec{e}_z\)
Énergie mécanique
Définition
L'énergie mécanique correspond à la somme de l'énergie cinétique et de l'énergie potentielle \[E_m = E_c + E_m\]
- Si il n'y a pas de forces non conservatives, alors, la variation de l'énergie mécanique est nulle \[\Delta E_m = 0\] soit \(E_m(A) = E_m(B\))
- Si il y a des forces non conservatives2, alors la variation de l'énergie mécanique est \[\Delta E_m = \sum_i W_{A \to B} (\vec{F}_{NC,i})\]
Conséquence
La variation d'énergie potentielle d'un système est \[\Delta E_p = -W_{A \to B}(\vec{F}_{C})\]
Preuve : \[\Delta E_m = \Delta E_c + \Delta E_p,\] \[W(F_{NC}) = W(F_{NC}) + W(F_{C}) + \Delta E_p,\] soit \(\Delta E_p = -W(F_C)\quad \blacksquare\)
Exercices
Un balle est lâchée depuis une altitude zA = 1,0 m sans vitesse initiale, elle arrive quelques instant plus tard a une altitude zB = 0 m juste avant de toucher le sol. On fait l'hypothèse qu'elle n'est soumise qu'a son poids.
- Déterminer la valeur de l'énergie cinétique au point A.
- Exprimer puis calculer l'énergie potentielle de pesanteur au point A.
- Déterminer la valeur de l'énergie potentielle au point B.
- Exprimer puis calculer la vitesse de la balle au point B.
15, 17, 24, 25, 26, 27 p 269-2733
Résumé
Carte mentale